Clusterverfahren - k-Means und die Bestimmung der optimalen Clusteranzahl (Part 3)
Dieser Beitrag ist eine Fortsetzung des zweiten Beitrags aus der Reihe Clustering. Darin wurde erklärt, wie man die Qualität eines Clusterings messen kann, obwohl wir uns im Bereich des Unsupervised Learnings befinden. Dieses Qualitätsmaß (Quality Ratio) bzw. Teile davon kann man auch dazu verwenden, die optimale Anzahl an Cluster zu bestimmen. Im Folgenden wird gezeigt, wieso die Bestimmung der Clusteranzahl überhaupt ein Problem ist und ein möglicher Lösungsweg zur Bestimmung beschrieben.
Kriterium zur Bestimmung der Anzahl von Cluster
Wir erinnern uns an die Quality Ratio, die im letzten Blogbeitrag beschrieben wurde:
.
Wir könnten nun dieses Maß dafür heranziehen, um die optimale Anzahl von Clustern zu bestimmen. Da Mathematiker an sich aber rechenfaul sind, reicht es aus, die tot.withinss (Summe der quadratischen Abweichungen der Punkte zu ihren jeweiligen Clusterzentren) zu berechnen. Dies ist möglich, da die Minimierung dieser Größe automatisch auch die betweenss (gewichtete Summe der quadratischen Abweichungen der Zentren zum globalen Zentrum) maximiert. Beide Richtungen führen dazu, dass die Quality Ratio gegen 1 also 100% Qualität geht. Wieso aber reicht eine einfache Minimierung der tot.withinss nicht?
Praktisch optimal - gibt´s nicht!
Zunächst schauen wir uns anhand eines Beispiels die Ergebnisse für ein Clustering mit einem Cluster und mit n (Anzahl der Datenpunkte) Clustern an. Dazu sei der Datensatz wie folgt aufgebaut mit 110 Datenpunkten:
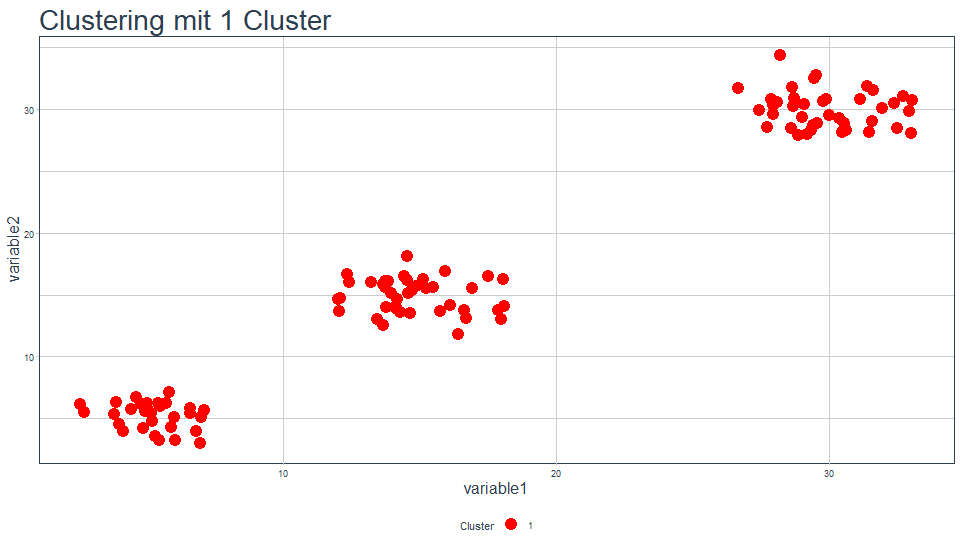
Geben wir vor, dass der Algorithmus die Punkte in genau ein Cluster clustern soll, haben wir aus zwei Gründen das Ziel (sinnvolle Abstrahierung der Daten) nicht erreicht. Erstens gibt es keine Abstrahierung und zweitens ist die tot.withinss maximal, genauer hier: 22472. Führen wir ein Clustering durch, für das wir die Anzahl an Clustern auf die Anzahl der Punkte setzen, erhalten wir genau 110 Cluster mit dem jeweiligen Punkt als Zentrum. Jedes Cluster besteht dann nur noch aus einem Punkt und hat somit keine Abweichungen innerhalb des Clusters, tot.withinss ist 0:
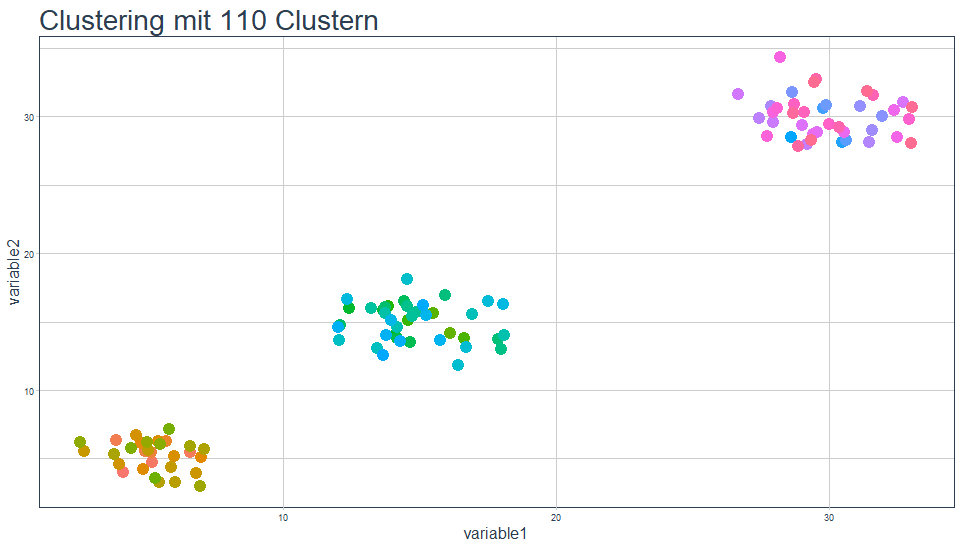
Würden wir also tot.withinss einfach stur minimieren, erhalten wir keinen Mehrwert aus dem Clustering. Rein mathematisch nach der Theorie wäre dies optimal. Rein praktisch gesehen, benötigen wir aber offensichtlich eine Anzahl an Cluster, die auf der einen Seite nicht zu groß ist (sinnvolle Abstrahierung der Daten), andererseits aber die tot.withinss möglichst klein hält. Praktisch ist also eine Lösung zwischen 1 und n Cluster am sinnvollsten. Dies erreichen wir z.B. mit der Ellbow-Method, auf die wir nun näher eingehen.
Die Erlösung: Ellbow-Method
Oben haben wir beschlossen, die tot.withinss als Maß für die Bestimmung der optimalen Clusteranzahl heranzuziehen. Zudem wissen wir über diese Größe, dass sie mit einer wachsenden Clusteranzahl gegen 0 geht und stetig fallend ist1. Nun könnten wir das Clustering einfach bis zu einer beliebigen Anzahl an Cluster Schritt für Schritt durchlaufen lassen und die Ergebnisse speichern (d.h. Clustering mit einem Cluster, Clustering mit zwei Cluster, etc.). Damit erhalten wir:
 |
 |
 |
 |
 |
 |
 |
 |
 |
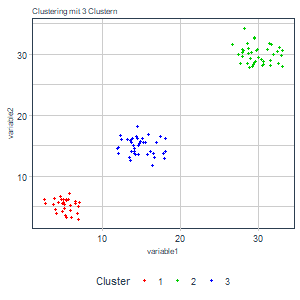
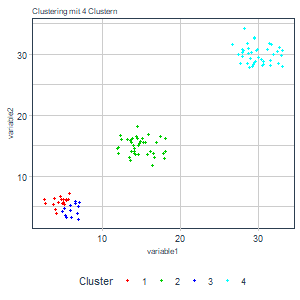
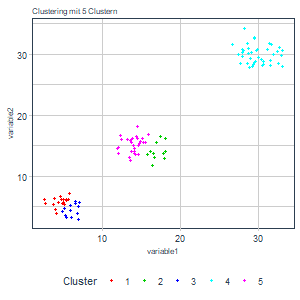
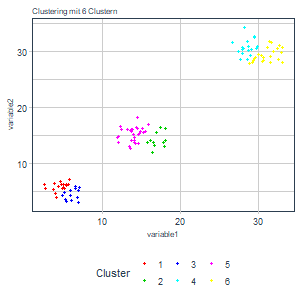
Aus den Grafiken lässt sich schon intuitiv ableiten, dass eine größere Anzahl an Cluster in diesem Beispiel vermutlich wenig Sinn macht. Neben den Ergebnissen haben wir aber auch die tot.withinss gespeichert und können diese auch gegen die Anzahl der Cluster plotten:
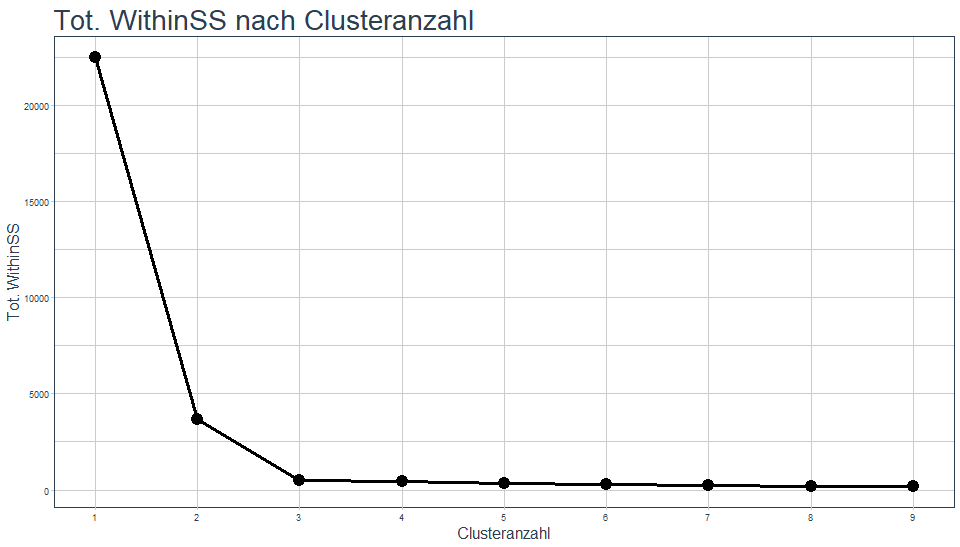
Man sieht eine zunächst stark fallende und dann sehr abrupt abflachende Funktion mit steigender Clusteranzahl. Da wir eine tot.withinss nahe bei 0 erzielen wollen, können wir einen solchen Abfall des Graphen als Informations- bzw. Abstraktionsgewinn interpretieren. Wechseln wir von einem Cluster auf zwei oder von zwei auf drei haben wir einen starken Informationsgewinn. Von drei Cluster zu vier Clustern und bei nachfolgenden Erhöhungen erhalten wir kaum noch sinnvolle Zusatzinformationen. Wir würden also den Punkt auswählen, bis zu diesem wir einen Gewinn haben. Das wäre in diesem Fall das Clustering mit drei Clustern. Nun wissen wir auch, woher der Name dieser Methode stammt.
Fazit
Wir haben gezeigt, wie man aus einer Mischung aus Theorie und intuitiven Ansätzen aus der Praxis eine optimale Anzahl an Clustern finden kann. Natürlich werden die Ergebnisse mit nicht konstruierten Daten nicht zwangsweise einen schönen Knick aufweisen. Es ist dennoch eine gute Methode, um die Anzahl der verwendeten Cluster zu plausibilisieren. Verwendet man Clustering automatisiert, ist man natürlich auf eine Funktion angewiesen, die aus dem Graphen die optimale Anzahl zieht oder andere Indikatoren heranzieht. So z.B. die R-Funktion Nbclust, die zahlreiche verschiedene Indizes und Kriterien zur Bestimmung heranzieht. Wir haben hier trotzdem die Ellbow-Method beschrieben, da sie sehr schön intuitiv erklärbar ist. Im nächsten Beitrag und dem letzten Kapitel zu k-Means Clustering werden wir die Startwertproblematik analysieren und Wege aus diesem Dilemma zeigen.
Bis dahin!
-
Stetig fallend zumindest im Bezug auf k-Means. ↩
