Clusterverfahren - k-Means und die Messung der Qualität (Part 2)
Dieser Beitrag ist eine Fortsetzung des ersten Beitrags aus der Reihe Clustering. Darin wurde erörtert, was das Ziel von Clustering ist und wie es sich zu anderen Herangehensweisen wie Segmentierung und Klassifikation unterscheidet. Anhand von Beispielen wurde zudem erklärt, auf welche Eigenheiten in den Daten der Nutzer Wert legen sollte. Drei weitere interessante Punkte der k-Means Methode wurden dabei nur erwähnt und sollen in den folgenden Beiträgen vertieft erkärt werden:
- Messung der Qualität
- Anzahl der Cluster
- Startwertproblematik.
In diesem Beitrag nehmen wir uns der Messung der Qualität eines Clusterings an. Dabei wird als Beispiel k-Means herangezogen und die Aussagen sind nicht auf alle Clusteralgorithmen anwendbar.
Quality Ratio - das Qualitätsmaß
Im Bereich des Supervised Learnings ist es leicht ein Fehler zu bestimmen (auch wenn die Auswahl des Fehlermaßes nicht immer trivial ist), da zu jeder Vorhersage auch ein tatsächlicher Wert gegenübersteht. Im Bereich Unsupervised Learnings, dem das Clustering und damit auch k-Means zuzuordnen ist , gibt es einen solchen tatsächlichen Wert nicht. Mann kann also im ersten Moment nicht klar sagen, welcher Clusteringversuch nun der bessere ist. Eine Herangehensweise, trotzdem einen Hinweis auf die Qualität zu bekommen, ist die Quality Ratio
.
totss ist die Summer aller quadratischen Abweichungen und lässt sich deshalb in die Summe von betweenss und tot.withinss aufsplitten. Dabei besteht der tot.withinss aus den Summen der quadratischen Abweichungen aller Punkte zum jeweiligen Clusterzentrum. Der betweenss gibt die Abstände (Summe quadratischer Abweichungen) der Zentren zum globalen Zentrum gewichtet nach der Größe der Cluster an.
Zur Plausibilisierung führen wir uns nochmal vor Augen, was das Ziel eines Clusterings ist. Es sollen Cluster identifiziert werden, die in sich möglichst homogen und untereinander möglichst inhomogen sind. Das bedeutet nichts anderes, als dass die Abstände der Punkte zu den jeweiligen Clusterzentren möglichst gering, die Clusterzentren aber möglichst weit auseinander sein sollten. Das mathematisch perfekte Clustering besteht als aus einem tot.withinss gleich 0 (keine Abweichungen zum Clusterzentrum). Damit erhalten wir eine Quality Ratio von 1 bzw. 100%.1 Ist der tot.withinss größer als 0, so sinkt die Quality Ratio gegen 0. Wir haben es hier also mit einem Maß zwischen 0 und 1 zu tun, was grundsätzlich sehr intuitiv ist.
Beispielrechnung
Das Ganze verifizieren wir nun anhand eines kleinen Beispiels.
Code
dt <- data.table(variable1 = c(1, 2, 3),
variable2 = c(1, 2, 3))
print(dt)
## variable1 variable2
## 1: 1 1
## 2: 2 2
## 3: 3 3
Grafisch sieht das Ganze so geclustert mit 2 Clustern wie folgt aus:
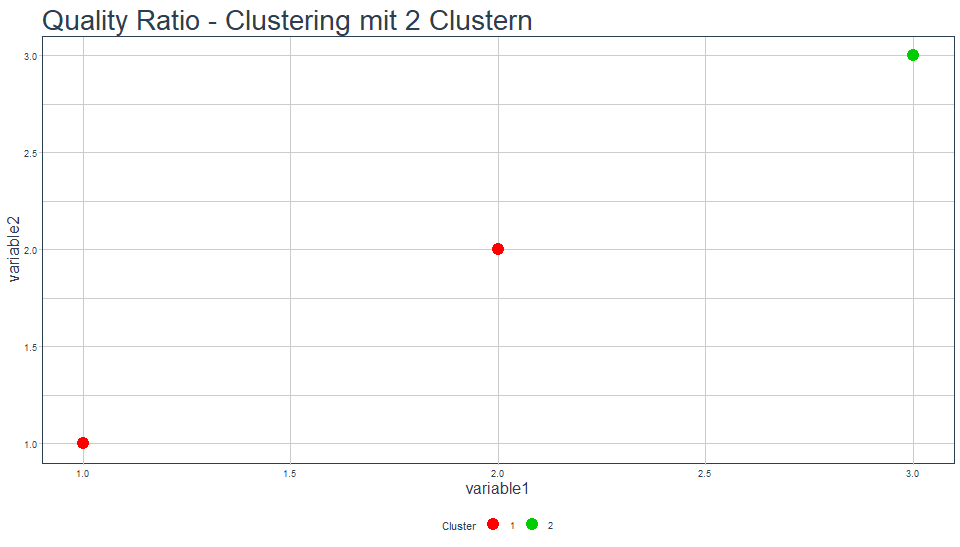
Für dieses Clustering erhalten wir eine Quality Ratio von 75%.2 Um das nachzuvollziehen, berechnen wir zunächst die tot.withinss. Das Zentrum für Cluster 1 ist mit den Punkten (1, 1) und (2, 2) ist (1.5, 1.5). Der quadratische Abstand der Punkte beträgt somit jeweils 0.5. In Summe erhalten wir eine withinss für dieses Cluster von 1. Das zweite Cluster hat eine withinss von 0, da es nur einen Punkt enthält. Die tot.withinss beträgt also 1. Die betweenss kann man entweder über die Distanzen der einzelnen Punkte berechnen, oder man berechnet die Abweichungen der quadratischen Summen über die Clusterzentren, gewichtet nach der Anzahl der Punkte im Cluster. In R können wir mithilfe der scale()-Funktion zentrieren, anschließend quadrieren und durch die Summen ans Ziel gelangen:
Code
set.seed(2)
dt <- data.table(variable1 = c(1, 2, 3),
variable2 = c(1, 2, 3))
k <- kmeans(x = dt, centers = 2)
sum(scale(k$center[k$cluster,], scale = FALSE)^2)
## [1] 3
Die betweenss ist also 3. Wenden wir nun die Formel für die Quality Ratio von oben an, erhalten wir
.
Clustering gut - nicht alles gut
Nachdem wir also wissen, wie man die Qualität eines Clusterings bestimmen kann, können wir ohne Bedenken mit Berücksichtigung der Quality Ratio das Clusterergebnis verbessern. Leider nicht ganz! Das Maß hat auch seine Tücken. Erstens ist es nur ein relatives Maß. Wir können nicht allgemein sagen, wie gut 75% sind. Der Vergleich zwischen verschiedenen Qualitäten kann aber angewendet werden - 75% ist besser als 70%. Zweitens haben wir das Problem, dass mit steigender Anzahl der Cluster der tot.withinss gegen 0 sinkt. Genau 0 ist tot.withinss dann, wenn es genauso viele Cluster wie Datenpunkte gibt. Dann entsprechen nämlich die Clusterzentren exakt den Datenpunkten und der Abstand eines jeden Datenpunktes zu seinem Zentrum ist somit 0. Wenn tot.withinss mit steigender Clusteranzahl aber gegen 0 geht, nähert sich die Quality Ratio der 1 bzw. 100% an. Der Nutzer könnte am Ende die Qualität des Clusterings beliebig durch die Clusteranzahl beeinflussen. Am Ende ist es jedoch nicht unser Ziel, möglichst viele Cluster zu erzeugen, sondern nur so viele wie benötigt werden, um zu abstahieren. Dieser Problematik und der Bestimmung der optimalen Anzahl an Cluster widmen wir uns im nächsten Teil der Clusteringreihe.
Fazit
Wir haben gesehen, dass es nicht ganz leicht ist, die Qualität eines Clusterings zu bestimmen. Wir erhalten jedoch einen relativen Wert, den wir zumindest zum Vergleich heranziehen können. Für Fuzzy-Cluster, in denen ein Punkt mehreren Clustern zugehörig sein kann oder ähnliche Verfahren, gilt diese Herangehensweise jedoch nicht. Im nächsten Beitrag befassen wir uns dann mit einer Möglichkeit, die optimale Anzahl an Clustern mit Hilfe der Quality Ratio zu bestimmen.
