Clusterverfahren - Einführung und k-Means in R (Part 1)
Einordnung und Abgrenzung
Immer wieder kann man die Worte Clusterverfahren, Cluster-Analyse und Clustering in falschen Zusammenhängen hören. Gerade im Boom der KI-Methoden werden oft Schlagwörter wild durcheinander geworfen, ohne sich deren Bedeutung genau bewusst zu sein. Dieser Blogbeitrag soll deshalb das Clustering klar von anderen Vorgehensweisen abgrenzen, die Vielfalt an Verfahren aufzeigen und eine kleine Einführung in einen der wohl bekanntesten Algorithmen, dem k-Means Algorithmus, geben.
Da mit Hilfe von Clusterverfahren ähnliche Strukturen identifiziert werden können, kann man sich vorstellen, dass diese in vielen Gebieten, von Medizin, Biologie und Physik, bis hin zur Betriebswirtschaft Anwendung finden. Man könnte im letzteren Gebiet z.B. seine Kunden clustern, um ähnliche Kundenstämme zu entdecken und mit diesen weiterführende Analysen durchführen. Nicht zu verwechseln sind Clusterverfahren mit einer Segmentierung und einer Klassifikation von Daten. Bei einer Segmentierung werden die Daten eher händisch mit vorgegebenen Grenzen bzgl. einer überschaubaren Menge an Kriterien eingeteilt. Dies geschieht z.B. bei rudimentären Kundenanalyse und der Einteilung in gut oder schlecht zahlende Kunden mit vordefinierten Bereichen. Diese Vorgehensweise stößt vor allem im Hinblick auf die Anzahl der implementierten Regeln an ihre Grenzen. Eine weitere Abgrenzung gibt es zur Klassifikation. Diese ist nicht wie Clusterverfahren dem Bereich des unsupervised learning, sondern vielmehr dem supervised learning zugeordnet. Hier besitzt man schon Daten, die einer Gruppe (Label) zugeordnet sind, kann darauf ein Modell entwickeln und z.B. neue Kunden direkt einer Gruppe zuordnen, obwohl diese noch gar keine Käufe getätigt haben. Die Aufgabenstellung weicht hier also komplett von der eines Clusterverfahrens ab. Jedoch kann letzteres als Input für die Klassifikation dienen, indem man zunächst ungelabelte Daten clustert und die identifizierten Gruppen als Label für eine Klassifikation heranzieht.
Clusterverfahren werden hauptsächlich in zwei Bereichen unterteilt, das Verfahren und die Gruppentypen.
Aufteilung der Verfahren:
- Partitionierend (jedes Cluster enthält eine disjunkte Menge an Punkten)
- Hierarchisch (jedes Cluster kann ein weiteres Cluster enthalten)
- Dichte-basierend (trennt Regionen mit hoher Dichte und niedriger Dichte)
- Verteilungs-basierend (teilt Punkte in verschieden verteilte Gruppen auf)
Aufteilung der Gruppentypen:
- Nicht überlappend (jeder Punkt ist in genau einem Cluster)
- Überlappend (Punkte können zu mehreren Clustern zugeordnet sein)
- Fuzzy (Punkte erhalten Gewichte, mit denen sie in die jeweiligen Cluster eingehen)
Ziel aller Clusterverfahren ist es, Gruppen zu identifizieren, die auf Grundlage der in den Algorithmus eingegangenen Werte, in sich möglichst homogen und gegeneinander möglichst heterogen sind. Punkte innerhalb einer Gruppe sollen also möglichst ähnliche Werte haben und zu anderen Gruppen möglichst starke Abweichungen aufweisen.
Genug Theorie - Wie funktioniert k-Means?
Der wohl bekannteste Clustering Algorithmus ist k-Means. Dieser ist der Gruppe der partitionierenden Verfahren mit nicht überlappenden Clustern zuzuordnen. Da das Verfahren auf den euklidischen Abstand beruht, können nur numerische Variablen berücksichtigt werden. Im Allgemeinen ist das Vorgehen wie folgt:
- Setze k Mittelwerte fest
- Zuordnung jeden Punktes zu dem nähesten Mittelwert
- Berechne pro Cluster den neuen Mittelwert
- Wiederhole Schritt 2 und 3 solange, bis kein Punkt mehr das Cluster ändert
Dies ist der Algorithmus von Lloyd1. In der Funktion kmeans in R wird der Algorithmus von Hartigon und Wong2 herangezogen. Dieser weicht leicht im Bezug auf die Update-Regel der Clustermittelwerte ab. Wie man schön im ersten Punkt sehen kann, gibt es zwei Eingabewerte für einen k-Means. Zum einen muss die Anzahl der Cluster vorgegeben werden, zum anderen die Orte der Startpunkte für die Mittelwerte (falls nicht angegeben, werden diese zufällig gesetzt). Zu diesen beiden Punkten und zu der Messung der Qualität eines Clusterings kommen wir in einem weiterführenden Blogbeitrag.
Im Folgenden sehen wir zufällig erstellte Daten, die in vorgegebene drei Cluster eingeteilt werden. Sind alle Voraussetzungen an diese Daten erfüllt (siehe unten mehr dazu), funktioniert k-Means sehr gut. Die untenstehenden Plausibilisierungen und Berechnungen wurden alle mittels R-Code umgesetzt.
Code
set.seed(100)
dt <- data.table(variable1 = c(rnorm(500, 1, 1), rnorm(500, 15, 1), rnorm(500, 8, 1)),
variable2 = c(rnorm(500, 1, 1), rnorm(500, 12, 1), rnorm(500, 7, 1)))
dt$cluster <- kmeans(x = dt, centers = 3)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Clustering - alle Voraussetzungen erf\u00fcllt")
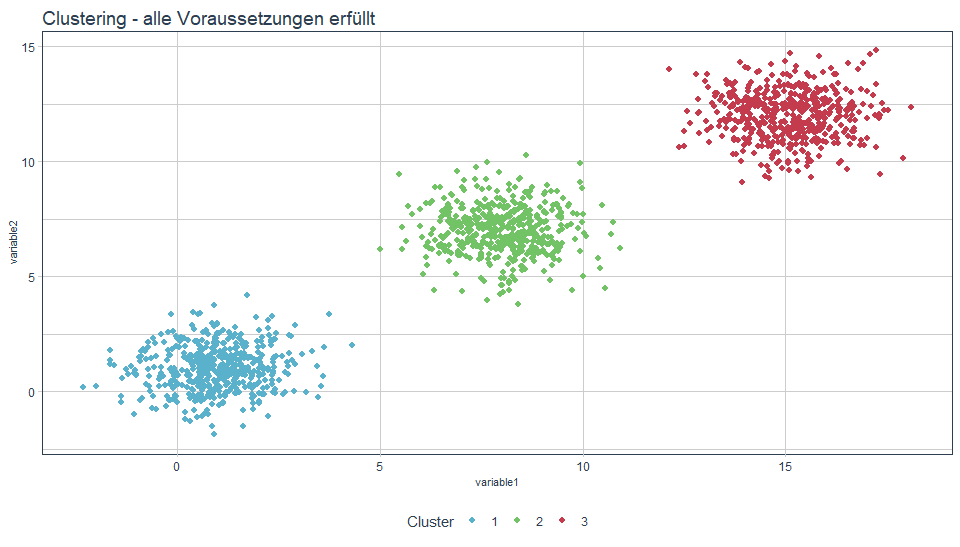
Sensibilisierung der Voraussetzungen
Auch wenn das Verfahren relativ simpel ist, gibt es dennoch einige Voraussetzungen an die Daten, um sinnvolle Ergebnisse zu erhalten:
- keine Ausreißer (Daten dürfen keine von der Masse stark abweichenden Punkte enthalten)
- gleiche Varianz der Variablen (die Verteilung der einzelnen Dimensionen darf nicht zu stark abweichen)
- keine kategorischen Variablen (alle Dimensionen sollten stetig und nicht diskret sein)
Im Folgenden werden alle Voraussetzungen mit Beispielen erklärt und dargestellt, wie k-Means bei Nichterfüllung der jeweiligen Voraussetzung reagiert.
Ausreißer
Wie in folgendem Plot dargestellt, befindet sich in den Daten ein Ausreißer.
Code
set.seed(100)
dt <- data.table(variable1 = c(rnorm(1000, 1, 1), rnorm(1000, 10, 1), 200),
variable2 = c(rnorm(1000, 1, 1), rnorm(1000, 10, 1), 10))
print(ggplot(data = dt, aes(x = variable1, y = variable2)) +
geom_point(pch = 20, size = 3) +
ggtitle("Ausreißer") +
theme_tq() +
theme(plot.title = element_text(size = 14),
axis.title = element_text(size = 8)))
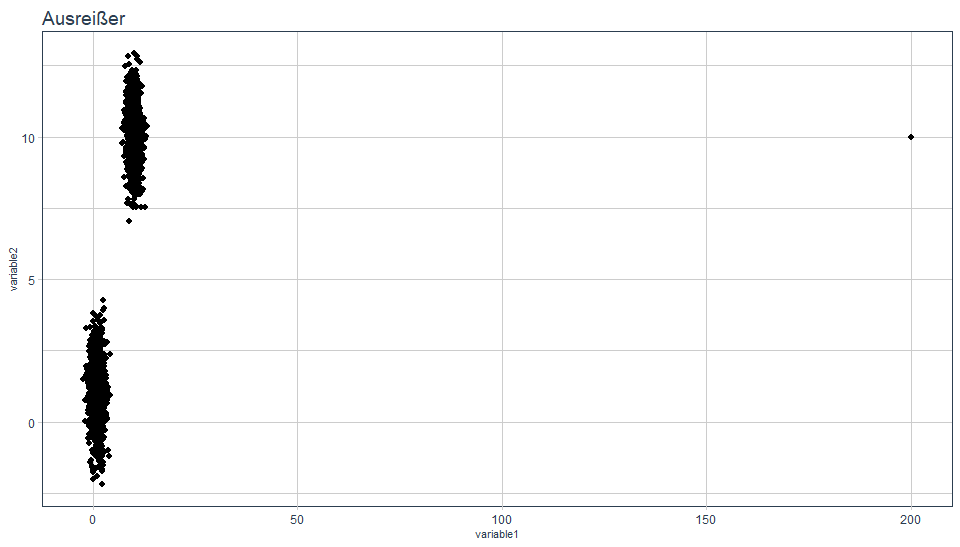
Was passiert nun, wenn wir diese Daten clustern wollen?
Geben wir 2 Cluster vor, so wird der Ausreißer zu einem der “offensichtlichen” Clustern zugeordnet. Die Interpretation von Cluster 2 könnte nun irreführende Ergebnisse erhalten.
Code
set.seed(100)
dt <- data.table(variable1 = c(rnorm(1000, 1, 1), rnorm(1000, 10, 1), 200),
variable2 = c(rnorm(1000, 1, 1), rnorm(1000, 10, 1), 10))
dt$cluster <- kmeans(x = dt, centers = 2)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Ausrei\u00dfer mit 2 Cluster")
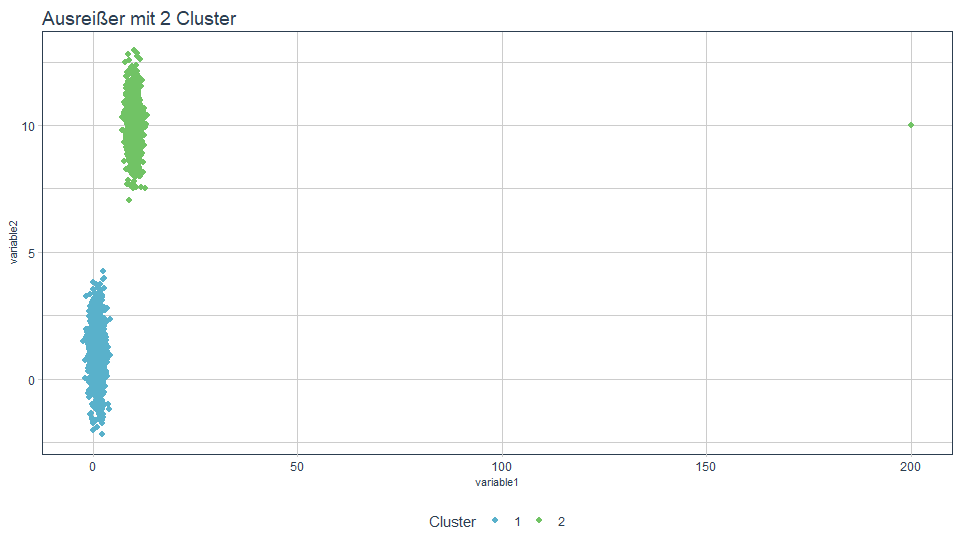
Geben wir 3 Cluster vor, kann es je nach Daten auch zu unterschiedlichen Ergebnissen führen.
Code
set.seed(15)
dt$cluster <- kmeans(x = dt, centers = 3)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Ausrei\u00dfer mit 3 Cluster (Teil 1)")
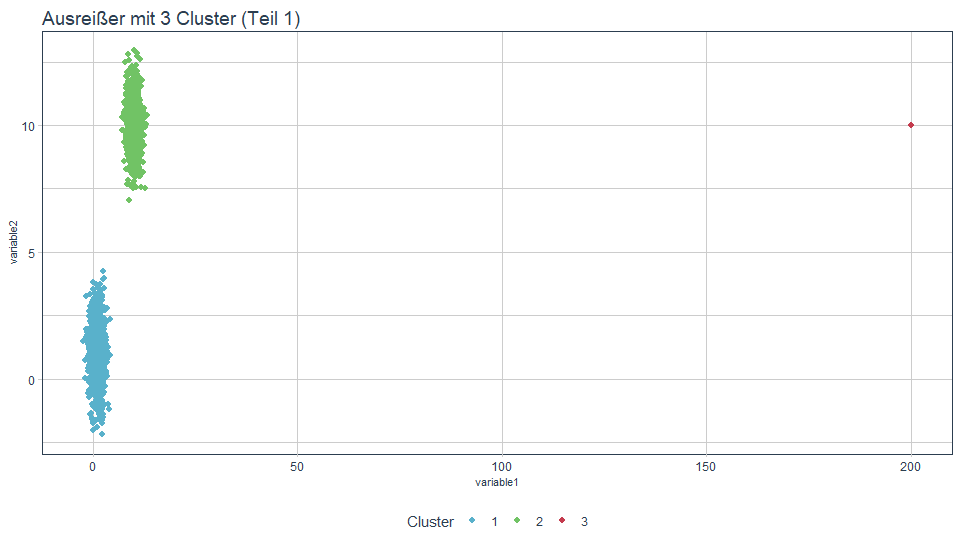
Code
set.seed(222)
dt$cluster <- kmeans(x = dt, centers = 3)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Ausrei\u00dfer mit 3 Cluster (Teil 2)")
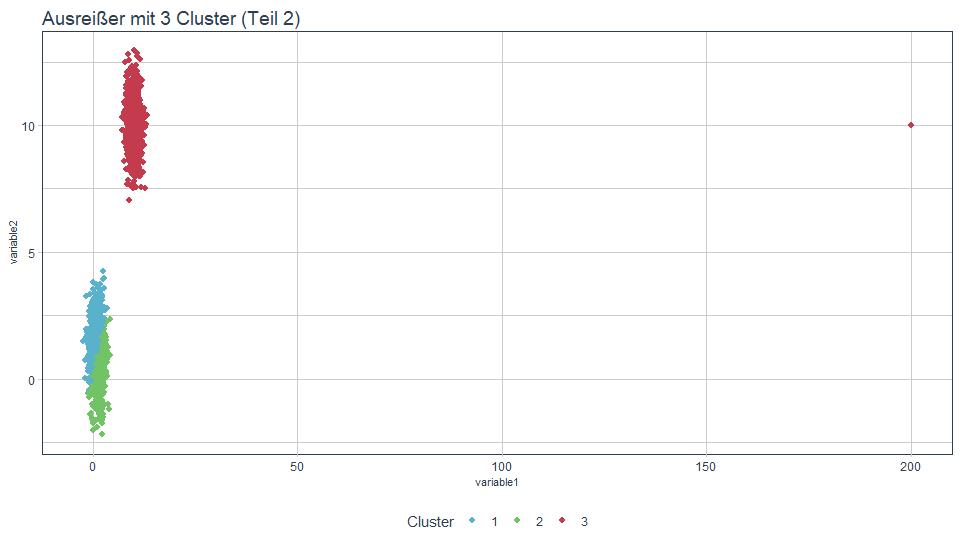
Mit der zweiten Grafik könnten wir deutich besser leben. Es ist jedoch aufgrund der Startwertproblematik nicht sichergestellt, dass wir dieses Ergebnis immer erhalten.
Wenn wir den Ausreißer jedoch entfernen, erhalten wir mit 2 Clustern wieder ein plausibles und interpretierbares Ergebnis.
Code
set.seed(222)
dt <- dt[-nrow(dt)]
dt$cluster <- kmeans(x = dt, centers = 2)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Ausrei\u00dfer entfernt")
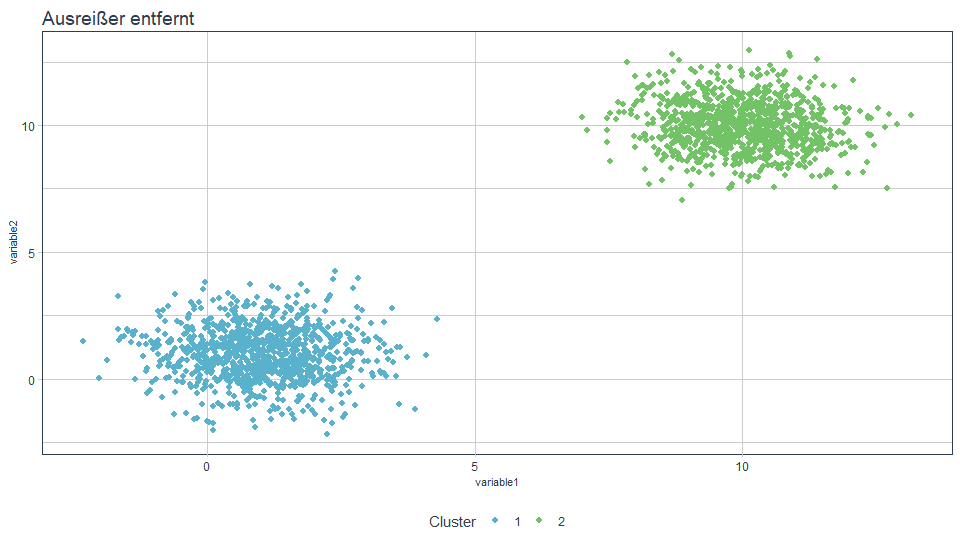
Unterschiedliche Varianz
Ein weiteres Problem stellen unterschiedliche Varianzen in den Daten dar. Variable 1 hat eine deutlich höhere Varianz als Variable 2.
Code
set.seed(100)
dt <- data.table(variable1 = c(rnorm(1000, 1, 300)),
variable2 = c(rnorm(500, 1, 0.5), rnorm(500, 5, 0.5)))
dt$cluster <- kmeans(x = dt, centers = 2)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Unterschiedliche Varianz")
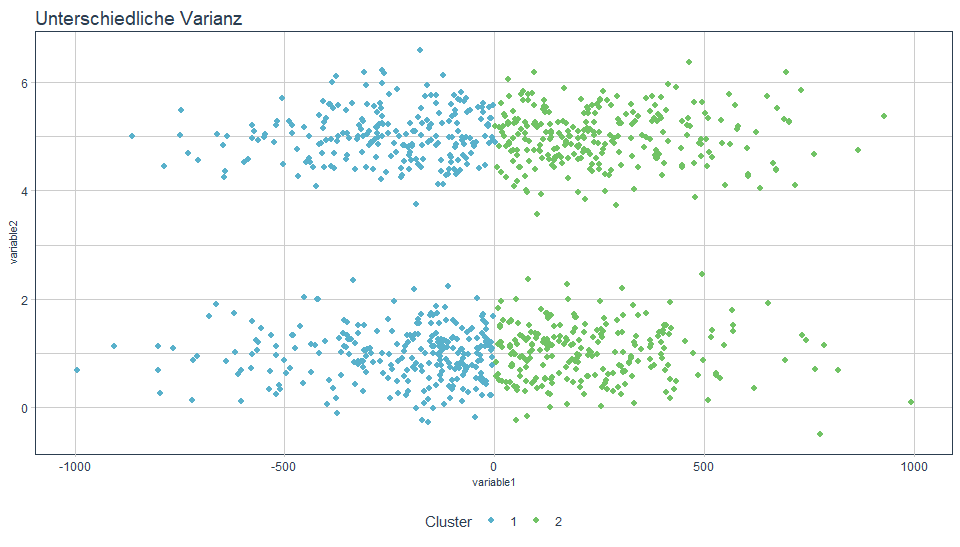
Wie man sieht, wird die Variable mit der höheren Varianz (variable1) bevorzugt bzw. stärker gewichtet. Das bedeutet, die Trennung erfolgt hier eher vertikal. Wieso ist das so? Dazu führt man sich die Zielfunktion, Minimierung des euklidischen Abstandes also Minimierung von quadratischen Abweichungen, vor Augen. Hohe Abweichungen werden durch die Quadrierung noch einmal viel stärker bestraft, als geringe Abweichungen. Daher versucht k-Means besonders auf der Achse von Variable 1 die Abstände zu minimieren, was zu einer vertikalen Trennung der Daten führt. Beheben lässt sich dies in den meisten Fällen durch eine Normalisierung der Daten. Eine Methode, die sicher datenunabhängig funktioniert, ist die Standardisierung.
Code
dt$variable1Standardized <- (dt$variable1 - mean(dt$variable1)) / sd(dt$variable1)
dt$variable2Standardized <- (dt$variable2 - mean(dt$variable2)) / sd(dt$variable2)
dt$cluster <- kmeans(x = dt[, list(variable1Standardized, variable2Standardized)], centers = 2)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1Standardized",
column2 = "variable2Standardized",
title = "Unterschiedliche Varianz (standardisiert)")
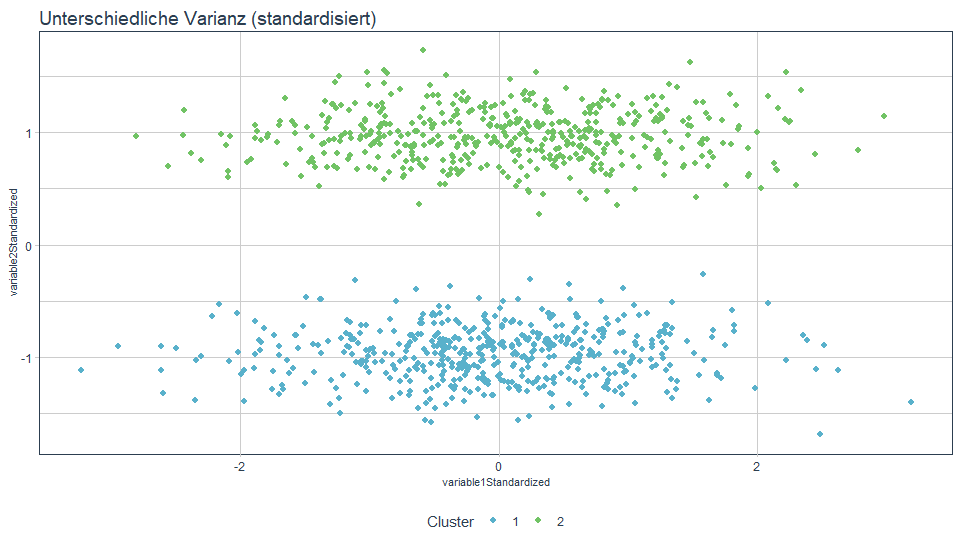
Mit den standardisierten Dimensionen erhalten wir nun das für uns intuitivere Ergebnis.
Kategorische Variablen - nicht sinnvoll
Da k-Means Abstände berechnet, ist es wenig sinnvoll kategorische Variablen in Form von diskreten Werten (1, 2, 3…) im Algorithmus zu berücksichtigen.
Code
set.seed(100)
dt <- data.table(variable1 = rnorm(1000, 100, 7),
variable2 = sample(c(0, 1, 2), size = 1000, replace = TRUE))
dt$cluster <- kmeans(x = dt, centers = 3)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1",
column2 = "variable2",
title = "Kategorische Variablen")
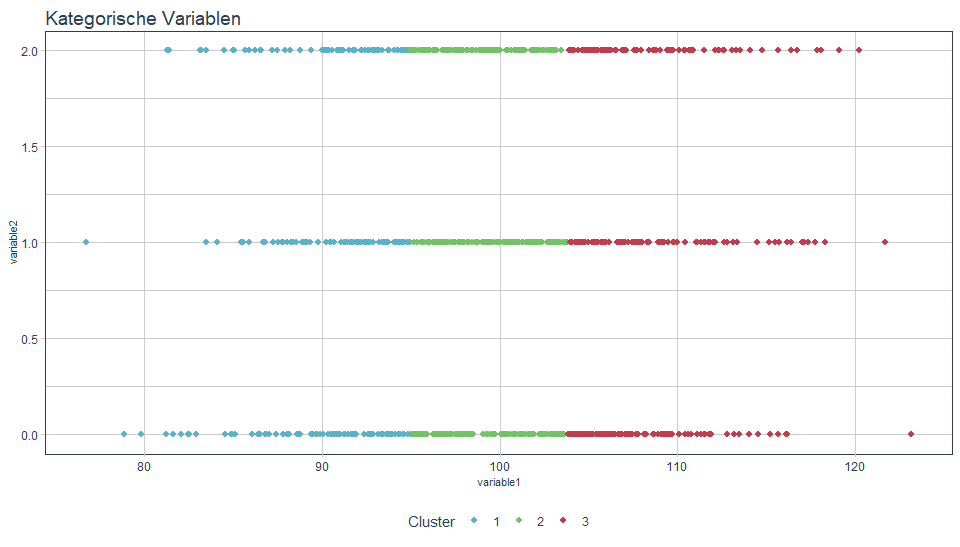
Hier tritt z.B. das Phänomen der unterschiedlichen Varianzen wieder auf. Auch normalisiert lässt sich dies nicht wirklich sinnvoll lösen.
Code
dt$variable1Normalized <- (dt$variable1 - min(dt$variable1)) / abs(max(dt$variable1) - min(dt$variable1))
dt$variable2Normalized <- (dt$variable2 - min(dt$variable2)) / abs(max(dt$variable2) - min(dt$variable2))
set.seed(100)
dt$cluster <- kmeans(x = dt[, list(variable1Normalized, variable2Normalized)], centers = 3)$cluster
plotKMeans(dt = orderCluster(dt, "variable1", "variable2"),
column1 = "variable1Normalized",
column2 = "variable2Normalized",
title = "Kategorische Variablen (standardisiert)")
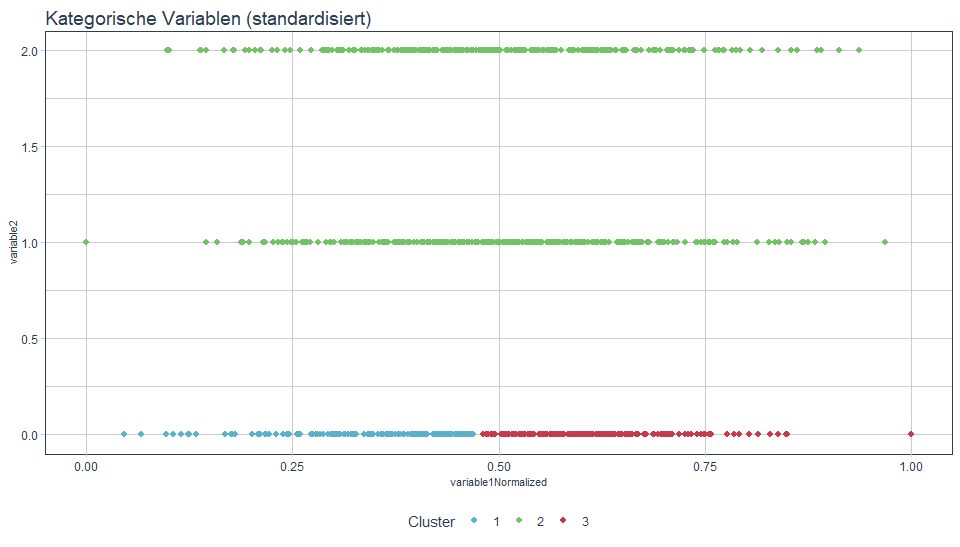
Fazit
Clusterverfahren sind ein fester Bestandteil in der Datenanalyse und können neue Einblicke in Daten geben. Wie bei allen Algorithmen benötigt man dafür aber auch ein detailliertes Verständnis, um sie richtig einzusetzen. Dies wurde anhand von k-Means gezeigt, der in sich ziemlich schlüssig und einfach erklärbar ist. Jedoch ist dies keine Garantie dafür, dass er gute Ergebnisse liefert. Es lohnt sich also allemal, auf die oben dargestellten Voraussetzungen zu prüfen und die Daten gegebenenfalls anzugleichen. Aber nicht alle Verfahren haben diese Probleme. So können z.B. dichte-basierende Verfahren Ausreißer berücksichtigen (DBSCAN). Einer Erweiterung von k-Means, dem PAM (k-Medoids) - Algorithmus, können auch andere Distanzfunktionen übergeben werden. In einem nächsten Blogbeitrag soll genauer auf die Startwertproblematik, Auswahl der Startpunkte und die Messung der Qualität eingegangen werden.
Freut euch darauf!
Möchten Sie mehr darüber erfahren, wie wir (nicht nur) mit R Lösungen für unsere Kunden entwickeln? Wir freuen uns auf Ihre Anfrage!
